Publications

2023

1. 

   Generalized Narain Theories Decoded: Discussions on Eisenstein series, Characteristics, Orbifolds, Discriminants and Ensembles in any Dimension

   Meer Ashwinkumar, Abhiram Kidambi, Jacob M. Leedom, and 1 more author

   Nov 2023

   Abs HTML PDF

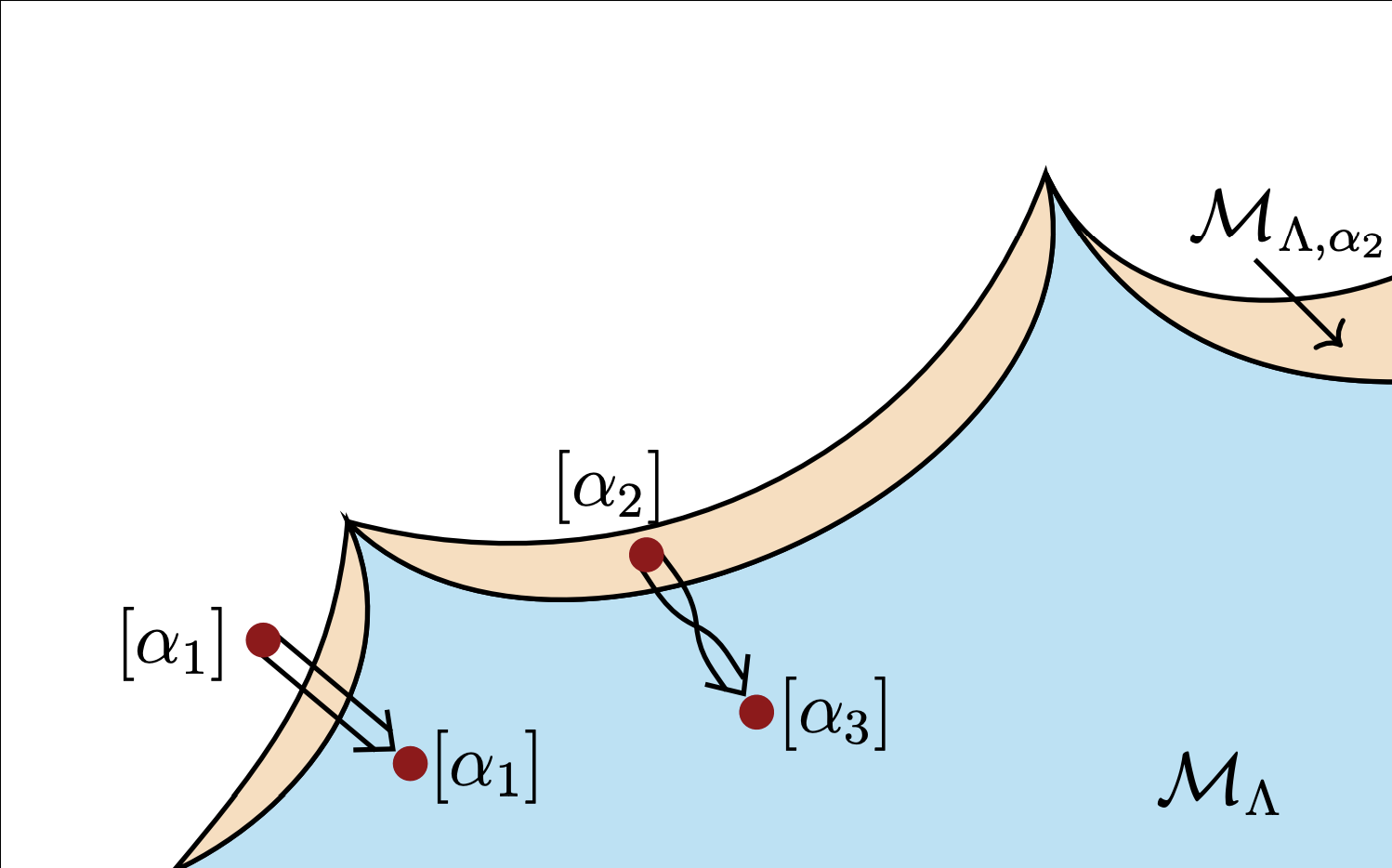
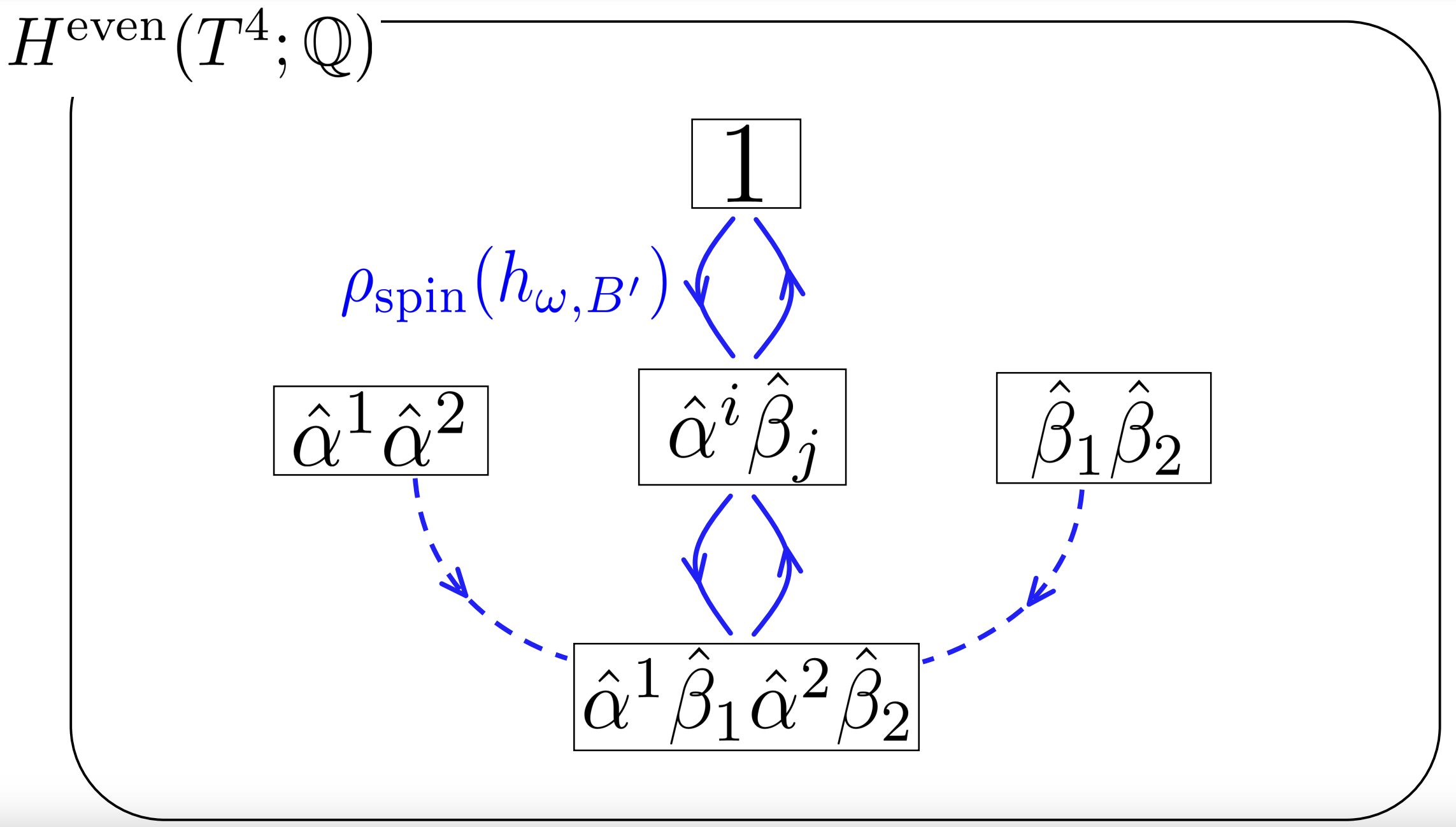
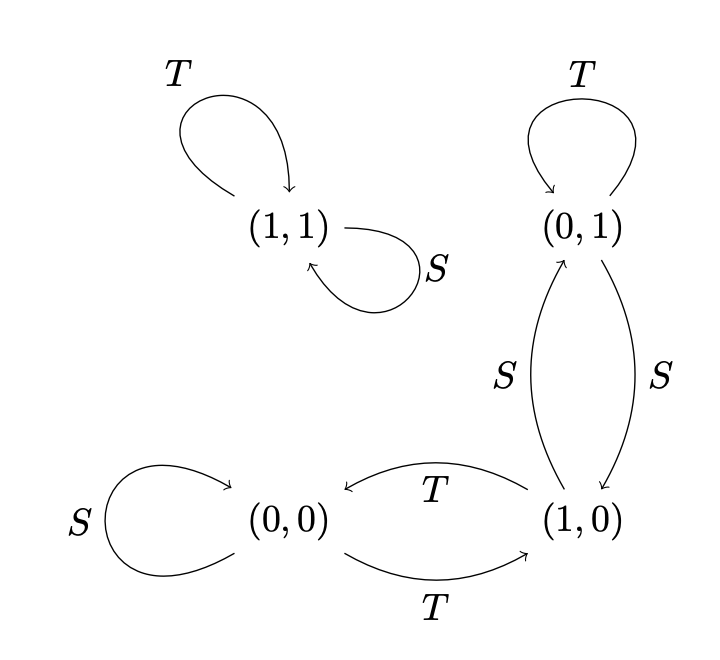
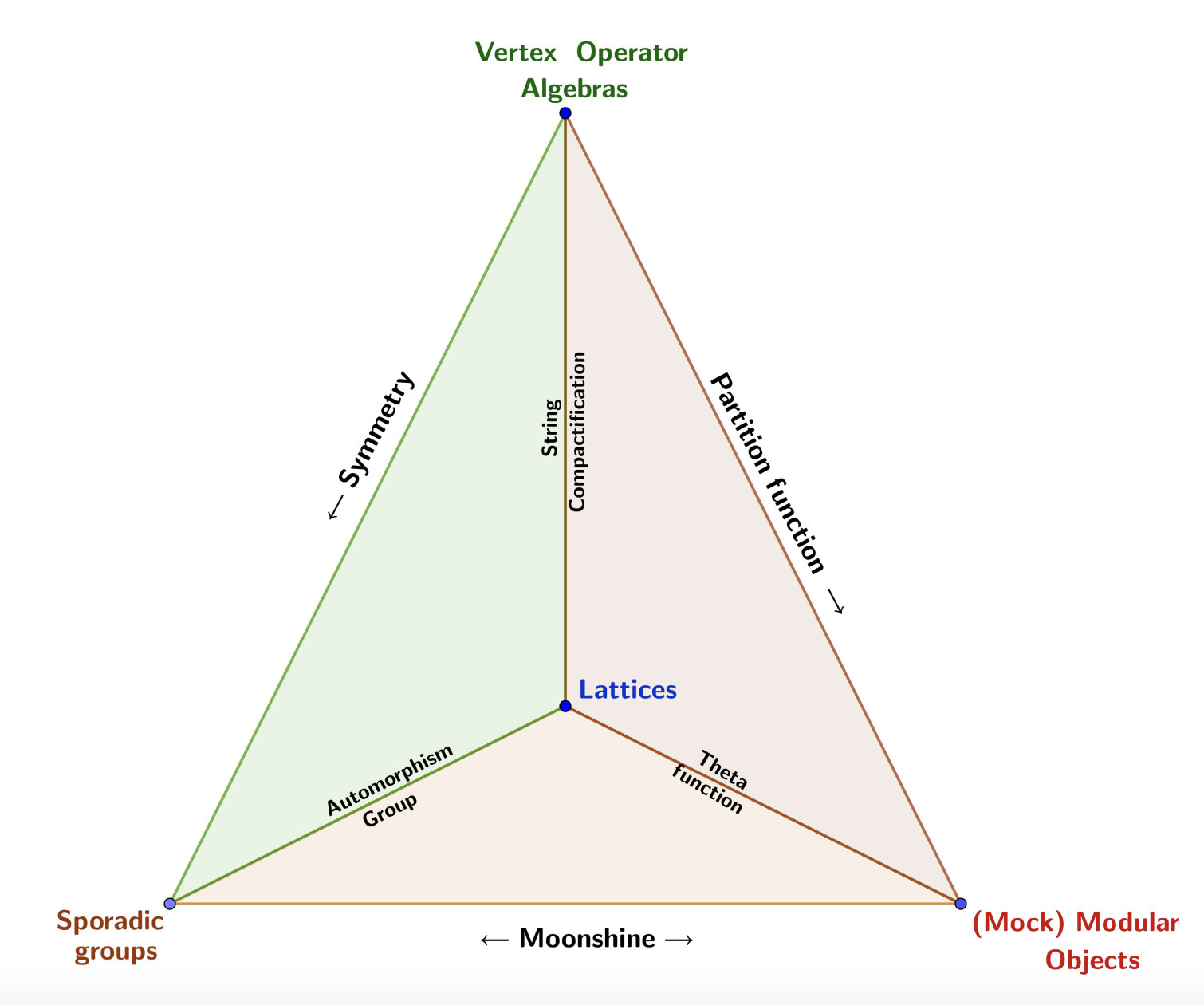
   We study a class of newly-introduced CFTs associated with even quadratic forms of general signature, which we call generalized Narain theories. We first summarize the properties of these theories. We then consider orbifolds of these theories, thereby obtaining a large class of non-supersymmetric CFTs with exactly marginal deformations. We then discuss ensemble averages of such theories over their moduli space, and obtain a modular form associated with the quadratic form and an element of the discriminant group. The modular form can be written as a Poincaré series, which contains novel invariants of lens spaces and suggests the interpretation of the holographic bulk as a theory of anyons.

2. The Gravitational Path Integral for N=4 BPS Black Holes from Black Hole Microstate Counting

   Gabriel Lopes Cardoso, Abhiram Kidambi, Suresh Nampuri, and 2 more authors

   Annales Henri Poincare, Nov 2023

   Abs HTML PDF

   We use the exact degeneracy formula of single-centred 1/4 BPS dyonic black holes with unit torsion in 4D N=4 toroidally compactified heterotic string theory to improve on the existing formulation of the corresponding quantum entropy function obtained using supersymmetric localization. The result takes the form of a sum over Euclidean backgrounds including orbifolds of the Euclidean AdS_2\times S^2 attractor geometry. Using an N=2 formalism, we determine the explicit form of the Abelian gauge potentials supporting these backgrounds. We further show how a rewriting of the degeneracy formula is amenable, at a semi-classical level, to a gravitational interpretation involving 2D Euclidean wormholes. This alternative picture is useful to elucidate different aspects of the gravitational path integral capturing the microstate degeneracies. We also comment on the relation between the associated 1D holographic models.

2022

1. Octonionic Magical Supergravity, Niemeier Lattices, and Exceptional and Hilbert Modular Forms

   Murat Gunaydin, and Abhiram Kidambi

   Sep 2022

   HTML PDF

2. 

   Towards Hodge Theoretic Characterizations of 2d Rational SCFTs

   Abhiram Kidambi, Masaki Okada, and Taizan Watari

   May 2022

   Abs HTML PDF

   The study of rational conformal field theories in the moduli space of conformal field theories is of particular interest since these theories correspond to points in moduli space where the algebraic and arithmetic structure are usually richer, while also being points where non–trivial physics occurs (such as in the study of attractor black holes and BPS states at rational points). This has led to various attempts to characterize and classify such rational points. In this paper, a conjectured characterization by Gukov–Vafa (Commun. Math. Phys. 246 (2004) 181) of rational conformal field theories whose target space is a Ricci flat Kaehler manifold is analyzed carefully for the case of toroidal compactifications. We refine the conjectured statement as well as making an effort to verify it, using T^4 compactification as a test case. Seven common properties in terms of Hodge theory (including complex multiplication) have been identified for T^4-target rational conformal field theories. By imposing a subset of the seven properties, however, there remain $ \mathcal N = (1, 1) $ SCFTs that are not rational. Open questions, implications and future lines of work are discussed.

2021

1. 

   Chern-Simons invariants from ensemble averages

   Meer Ashwinkumar, Matthew Dodelson, Abhiram Kidambi, and 2 more authors

   JHEP, May 2021

   HTML PDF

2020

1. On Mathieu moonshine and Gromov-Witten invariants

   Andreas Banlaki, Abhishek Chowdhury, Abhiram Kidambi, and 1 more author

   JHEP, May 2020

   HTML PDF
2. Heterotic strings on (K3\times T^2)/\mathbbZ_3 and their dual Calabi-Yau threefolds

   Andreas Banlaki, Aradhita Chattopadhyaya, Abhiram Kidambi, and 2 more authors

   JHEP, May 2020
3. Dyonic black hole degeneracies in \mathcalN = 4 string theory from Dabholkar-Harvey degeneracies

   Abhishek Chowdhury, Abhiram Kidambi, Sameer Murthy, and 2 more authors

   JHEP, May 2020

4. 

   Automorphic forms in string theory: From Moonshine to Wall Crossing

   Abhiram Mamandur Kidambi

   Vienna, Tech. U., May 2020

   HTML PDF

2018

1. Calabi-Yau manifolds and sporadic groups

   Andreas Banlaki, Abhishek Chowdhury, Abhiram Kidambi, and 3 more authors

   JHEP, May 2018